ベイズ推定法を用いた翼列設計用CFDの予測精度向上に関する試み

　　松井孝太朗，谷　直樹

PDFダウンロード

松井　孝太朗　航空・宇宙・防衛事業領域技術開発センター要素技術部
谷　　直樹　　航空・宇宙・防衛事業領域技術開発センター要素技術部　グループ長　博士（工学）

CFD ( Computational Fluid Dynamics ) は近年のジェットエンジン設計に必須の技術であり，その定量的予測精度向上が必要不可欠となってきている．本検討ではベイズ推定法を用いて試験結果を真値として乱流モデルパラメータのチューニングを行うことで，翼列の空力性能と内部流れの予測精度を向上させることができるかどうか検討を行った結果を述べる．

CFD ( Computational Fluid Dynamics ) is an essential tool for modern jet engine design, and accuracy improvement is also imperative for aerodynamic design. In this study, turbulence model tuning was carried out with Bayesian estimation comparing CFD results and experimental data. Validation calculations were carried out on cascade flow problems to clarify whether aerodynamic performance and internal flow predictions can be improved.

1.　緒言

CFDは20世紀後半に急激に技術開発が進み，今ではジェットエンジン設計になくてはならない技術の一つとなっている．かつては物理モデルと計算機能力の双方が不足していることで定量的予測が困難だったが，近年は計算機能力の向上によりLES ( Large Eddy Simulation ) ^{( 1 )} やRANS ( Reynolds Averaged Navier-Stokes ) とのハイブリッド法 ^{( 2 )} による高精度解析が多くなされるようになってきている．

LESやLES-RANSハイブリッド法は適切に使うことで高い精度を誇るが，使用する計算資源が膨大であり，設計に使うには一晩で手軽に結果が得られない欠点がある．このため，古典的なRANSが設計CFDではいまだに主力であるが，精度の面では劣る．補正モデル ^{( 3 )} を適用することで向上可能である点は知られているが，多くの補正モデルがあり適した組合せを選択することが困難である．また，RANSで使用している物理モデルの定数は比較的簡単な流れ場の検証結果を基に決められており，実際の翼列内部の複雑形状で適切に予測できているとは言い難い．

そこで，本検討では，設計用のRANS CFDに用いる乱流モデルに対して試験結果を基にベイズ推定法を適用してチューニングすることで，高精度化を試みた結果を報告する．まずは二次元翼列のコーナー流れに関するチューニングを実施して手法の妥当性検証を行う．その手法を用いて，より複雑な流れ場である多段翼列形態に関してチューニングを行うことで，多段翼列流れに関して精度を向上できるか検証を行う．

2.　解析手法

2.1　ベイズ推定法

本検討では，予測誤差も含めて考慮可能なベイズ推定法の一種であるMAP ( Maximum a Posteriori ) 推定 ^{( 4 )} を用いる．MAP推定は，試験・実験データ，もしくは高精度解析結果を正の結果dとして，最もその条件を満たすパラメータセットθを求める．

ここでP_posteriorは事後の確率分布で，今回はパラメータセットの精度の良しあしを表す分布となる．また，Ppriorはパラメータセットについての事前の確率分布である．そしてこれらをつなぐP_likelihoodは尤度(ゆうど)と呼ばれ，試験データなどと比較した際の，あるパラメータセットによる予測の確からしさを表す関数である．

尤度関数を直接導出するためには多くの解析が必要になり非現実的であるため，乱流モデル変数をパラメータセットθとして，着目するCFD解析結果に関するサロゲートモデルを構築して計算負荷を低減する．今回は乱流モデルのパラメータセットのチューニングでありパラメータ数も限られるため多項式カオス法 ^{( 5 )} を用いた．

ここでf ( x, ξ )はサロゲートモデルから予測される解析結果，a_iは多項式カオス法の係数で，パラメータセットのサンプリング点xで計算された評価値を基に決められる．また，ψ_iは基底関数，ξはパラメータセットのランダムサンプリング点である．本手法の詳しい説明は参考文献 ^{( 6 )} を参照いただきたい．

2.2　C F D

2.2.1　CFDソルバ

本検討では，過去に基礎的な題材から実機レベルの圧縮機まで多く検証されており，特性がよく分かっている点を考慮し，国立研究開発法人宇宙航空研究開発機構 ( JAXA ) が開発したCFDソルバUPACS ^{( 7 )} を用いた．UPACSは圧縮性を考慮した密度ベースソルバであり，多くの解析により検証されている．物理量はセル中心で定義され，古典的ではあるが安定性の高いRoeスキームを用いて数値流束を計算している．MUSCL内挿により移流に関しては最大三次の空間精度を，粘性項に関しては中心差分により二次の空間精度を有する．時間積分は局所時間刻みを適用した定常解析を実施し，Matrix Free Gauss-Seidel法を用いた．

2.2.2　乱流モデル

ジェットエンジン内部流れは高レイノルズ数流れであるため乱流の考慮が必須となる．今回は安定性が高く計算負荷が低いSpalart Allmaras ( SA ) モデルを用いた．

ここでρは密度，v_iは各方向の流速，x_iは座標値，Sはひずみ速度を表し，υ，υ_t，dはそれぞれ分子動粘性，乱流動粘性，壁距離を表す．今回はこのSAモデルの係数c_b1，c_b2，cw2，c_w3，c_v1，σ，κを対象としてベイズ推定法を用いてチューニングを行った．

3.　検証対象

3.1　実験結果

本チューニング手法を検証するため，過去にドイツのRWTH Aachen Universityにて実施された遷音速直線翼列実験の結果 ^{( 8 )} を用いて，実験結果を真値として検討を行った結果を示す．第1図に直線翼列の概略図を示す．7 枚の翼を有する二次元直線翼列風洞であり，中心の翼とその上下の翼を計測対象として実験を行った．レイノルズ数は10⁶，入口マッハ数は0.7とし，どちらも実エンジンの環境に近い条件での試験となっている．入口全圧は0.135 MPa，入口全温は320 Kであり，入口乱流強度は3％となっている．32％軸コード長下流で5 孔ピトー管にて二次元分布の計測を実施している．入口流れ角が54.5°の条件のものをこれ以降のチューニング作業に適用した．

3.2　CFD解析

CFD解析コードは前述したJAXAにて開発されたUPACSを内部流向けに改修したものを利用した．

境界条件については，入口は全圧，全温度，流れ角，乱流粘性を固定し，乱流粘性以外は実験データに応じた分布を与えた．乱流粘性に関しては層流粘性の0.1倍のほぼ層流状態での流入を与えた．格子点数は700 万点であり，壁近傍格子幅に関しては粘性低層を適切に解像できる幅を設定している．

4.　ベイズ推定法によるチューニング

4.1　感度解析

今回のチューニングプロセスの概略を第2図に示す．対象となるパラメータはcb1，c_b2，c_w2，c_w3，c_v1，σ，κの七つであるが，多項式カオス法でサロゲートモデルを構築する際にすべてのパラメータに関して検討を行うと解析ケース数が膨大となるため，最初に感度解析を行って感度が大きいパラメータの抽出を行った．感度解析は各パラメータのデフォルト設定値の100～200％の幅で振って検討を行い，そのなかで結果のばらつきが大きい上位二つを選出した．なお，パラメータ範囲を100％以上の値で振ったのは，デフォルト設定値以下にすると解析が不安定になるケースが多く非物理的な解が得られたためである．

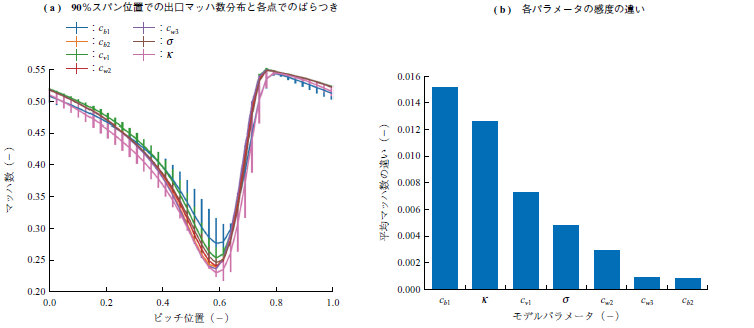
第3図に90％スパン位置での出口マッハ数分布の比較と，各パラメータを振った際のばらつき幅を示す．ここではコーナー流れに関してチューニングを行うので，その影響の表れる90％スパンに着目した．第3図 - ( a ) に示すとおり，最も低いマッハ数を示すピッチ位置は0.6近傍で大きくは変わらないが，ばらつきの幅，中央値の分布については違いが見られる．第3図 - ( b ) に見られるとおり，ばらつきの幅の大きいのはc_b1とκの二つであり，今回はこの二つのパラメータに関して多項式カオス法でのサロゲートモデル構築と，ベイズ推定法を適用したチューニングを進めた．

4.2　サロゲートモデル構築

2. 1節で述べたとおり，サロゲートモデルには多項式カオス法を用いた．感度の高い二つのパラメータc_b1，κについて，四次の多項式展開を用いてサロゲートモデルを構築した．第4図に解析を行ったパラメータ点を示す．今回は四次の多項式を用いるため，一つのパラメータ当たり5 水準，合計25 ケースの解析を実施した．この結果を用いてサロゲートモデルを構築し，サロゲートモデル上でランダムサンプリングして評価を行った．

今回のサロゲートモデルによって予測された結果のばらつきの幅を第5図に示す．評価する結果は第3図と同様に90％スパン位置のマッハ数分布とし，実験結果を真値としてチューニングを行う．「実験結果と合う」という指標をどのようにするかという点に任意性があるが，今回は下記2 段階のプロセスを踏むこととした．まず，第6図に示すように各ピッチ位置の点でマッハ数に関するサロゲートモデルを構築し，サロゲートモデル上にてランダムサンプリングを行い，多項式カオスによる予測値の確率密度関数を求める．次に尤度分布を求めて各点の最適解が得られるパラメータセットを予測した ．この結果では各点でばらつきのあるチューニング結果となるため，これらを全体的な分布が一致するように，ベイズ推定の原理も応用して各点の確率密度を掛け合わせることで分布全体に関する尤度，そして事後確率分布を求めた．なお，事前確率については計測誤差に相当する値を一様に与えた．その結果を第7図に示すが，c_b1 = 0.268，κ= 0.44で最適解が得られる結果となった．パラメータ設定範囲の隅の点であり，より大域的にパラメータを振ることでより良い解がある可能性もあるが，本章では手法の妥当性検証が主目的であるためこの値を用いた．

4.3　チューニング結果検証

ここまでの結果で最適解と思われるパラメータセットを導出できたが，実際に再計算を行うことで一致度が向上したか確認を行う．

再計算は，デフォルトのパラメータセットと，今回のチューニング結果を適用した結果の比較を実施した．第8図に出口のマッハ数分布を示すが，全体的な分布に関しては大きな違いが見られない．しかし，第9図に示す90％スパンのマッハ数分布では，チューニング後の結果はほぼ実験値と重なる結果が得られており，精度を大きく向上させるパラメータセットを示すことができた．

5.　翼列への適用

ここまでのプロセスでベイズ推定法と多項式カオス法を組み合わせることで，既存のCFDの予測精度を向上できる可能性を示すことができた．しかし，ここでの結果は比較的単純な二次元翼列形態であり，実際のジェットエンジンに近い多段翼列形態での検証が必要不可欠であることから，過去に実施された3.5 段圧縮機に関して検討を行った．

5.1　対　　象

今回対象としたのは，内部流計測や可視化が詳細になされており特性が一般的によく知られているアメリカのPurdue Universityの3.5段圧縮機 ^{( 9 )}で，第10図に形状を示す．解析は1流路のみを考えた定常解析を実施し，出入口は翼列から十分遠くに配置することで境界条件の影響を排除するようにした．各翼列でのマッハ数，レイノルズ数を第1表に示す．過去の検討から翼根部のフィレットRおよび翼列間の隙間を考慮し，総格子点数は1500万点となっている．

利用したCFDコードについては検証で用いたUPACSと同じものであるが，乱流モデルに関しては多段翼列問題に対して精度が良いSA-R-H-QCRモデルを適用した ^{( 3 )}．

ここでu，Ωはそれぞれ絶対座標系での流速ベクトルと渦度ベクトルである．このモデルは，SAモデル（ ( 3 ) 式 ～ ( 8 ) 式）に翼端渦の剛体回転部分の過剰な乱流粘性生成を抑制するR補正（ ( 10 ) 式），乱流のバックスキャッタ現象を限定的に考慮可能なH補正（ ( 11 ) 式）を加え，流れ場の方程式にひずみ応力評価に非等方性をモデル化するQCR補正を入れたものである．これらのモデル定数については推奨値が幅のある形で公開されている，あるいは最適値が公開されておらず，検証例も少ないことから，今回の枠組みを適用して最適な値を求める．

5.2　チューニング

チューニングに関しては，これらの新しく加えられた補正モデルの係数C_rot，c_h1，c_h2の三つに着目して実施し，第2表に示す範囲でパラメータを振って検討を進めた．なお，QCR補正の係数に関しては乱流モデル自体のモデルではないため，今回のチューニング対象からは外している．

チューニング手順に関しては4 章で述べた手法を踏襲し，今回は合わせ込む評価結果に関しては失速流量で考えた．第11図に事後確率分布を示す．それぞれの二次元等高線は二つのパラメータに着目したときの確率分布を，一次元のグラフについては一つのパラメータのみに着目したときの確率分布を示している．このような結果から，最適解が得られるパラメータセットとしてC_rot = 3.0，c_h1 = 1.34，c_h2 = 1.81が得られた．なお，この最適値は三つのパラメータの組合せで最も良いものを選んでおり，各パラメータを個別に見ている第10図の一次元プロットで得られる結果とは違っている．

5.3　全体性能

まず全体性能に関して比較を実施した．試験結果に関してはデータが公開されている流量－圧縮比の比較のみとなる．第12図に示すように，試験結果と比較すると今回のチューニング技術で導出された最適パラメータセットの補正乱流モデルを用いることで，通常の広く利用されているSAモデルより低い流量まで解析ができていることが分かる．ほかの翼列でも同様の結果を得られており妥当なチューニングと判断した．

5.4　内部流れの比較

全体性能比較のみでは全く違う流れ場となっていても同じ結果を示す場合があることから，内部の流れ場も比較することで予測精度改善の妥当性に関して確認を行った．第13図にHL条件とPE条件での1 段静翼出口，2 段静翼出口の全圧Ptの分布を示す．なお，全圧については入口全圧Ptinで無次元化されている．PE条件ではSAとSA-R-H-QCRの相違は小さいが，HL条件の場合SA-R-H-QCRモデルでは適切にシュラウド側の全圧低下を1 段静翼出口で再現している．また，2 段静翼出口ではまだ双方の乱流モデルとも相違がある状態だが，SA-R-H-QCRモデルの方がより試験結果に近い分布となっている．第14図には1 段静翼出口でのHL条件での断面全圧分布を比較している．実験結果では翼端側で大きな低全圧領域が見られる．SAモデルではむしろ翼根側での低全圧領域が大きく，定性的な傾向が異なってしまっている．チューニング後のSA-R-H-QCRモデルでは実験結果と同じで翼端側で低全圧領域が大きくなっており，定性的な傾向でも一致度が向上することが分かる．

6.　まとめ

本報告ではベイズ推定法を乱流モデルのチューニングに適用した結果に関して，二次元直線翼列で技術自体の検証を行い，実形状に近い三次元の3.5 段圧縮機に適用して実証レベルを上げた検討を行った．その結果をまとめると次のようになる．

• 試験データを教師データとしたベイズ推定法を用いることで，直線翼列でのコーナー流れのマッハ数分布を改善させることができた．
• 同様の技術を3.5 段圧縮機に適用することで，全体性能，内部流れ双方の予測精度向上を確認することができた．

本手法の有効性は検証することができたが，場合によっては非物理的なパラメータセットが最適解としてでてきてしまう可能性をはらんでいる．利用に関しては慎重に検証を行う必要がある ^{( 6 )}．

―　謝　　辞　―

本検討を行うに当たり，JAXA賀澤順一氏からはUPACSの利用許諾のみならず技術面の多くの助言をいただいた．また，ベイズ推定法による予測技術構築に関してはアメリカのUniversity of Notre Dameのターボ機械研究所 ( Turbomachinery Laboratory ) のAleksandar Jemcov教授に多くの助力をいただいた．試験データに関してはRWTH Aachen University，Purdue Universityが所属するGUIdeコンソーシアム，Purdue Universityでの試験結果を活用させていただいた．ここに謝意を表す．

　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　

第64巻 第1号 特集 未来へのクロスロードに立つ技術開発
：サステナビリティからAI 活用まで