Ti-6Al-4V製ディスクの過回転バーストに至る終局限界評価

　　北村優太，津乗充良，山田剛久，北村祥之，牛田博久

PDFダウンロード

北村　優太　技術開発本部技術基盤センター数理工学グループ　主査　博士（工学）
津乗　充良　技術開発本部技術企画部　グループ長　博士（工学）
山田　剛久　技術開発本部技術基盤センター材料・構造グループ　グループ長　博士（工学）
北村　祥之　航空・宇宙・防衛事業領域技術開発センターエンジン技術部　グループ長
牛田　博久　航空・宇宙・防衛事業領域技術開発センター要素技術部　主査

航空エンジンにおいて，ディスク過回転時のバースト回転数の予測精度を向上させてディスクを軽量化することが，競争力強化の観点から期待されている．構造解析によるディスクバーストの予測精度向上のためには，破断までの材料の終局挙動をモデル化することが重要となる．本研究では，Ti-6Al-4V製ディスクを対象にデジタル画像相関法によって取得した高ひずみ領域までの応力ひずみ関係を用いた構造解析と，応力状態に依存する破断ひずみに基づく延性破壊クライテリアを用いて過回転バーストに至る終局限界評価を実施した．

In aero engines, it is expected to improve the prediction accuracy of the disk burst rotation speed under overspeed condition and reduce the weight of the disk. In order to improve the prediction accuracy of disk burst by structural analysis, it is important to model the ultimate behavior of the material until fracture. In this study, the ultimate limit state evaluation leading to overspeed burst was carried out by structural analysis for a Ti-6Al-4V disk. The stress-strain relationship up to the high-strain region obtained by the digital image correlation method and the ductile fracture criterion based on the fracture strain dependent on stress state were used in this evaluation.

1.　緒言

航空エンジンにおいて，ディスクやシャフトなど，破壊した場合にエンジンを安全に停止できない状態となる部品をLife Limited Part ( LLP ) と呼ぶ．LLPの破壊は大事故につながるおそれがあるため，その寿命に制限があり一定期間使用されると交換が必要となる．LLPを設計し実用化する際にはアメリカ連邦航空局の認証が必要であり，ディスクの認証では運用上の最大回転数の120％でバーストしないことなどが要求される ^{( 1 )}．また，認証の取得には，試験または解析によって要求を満足することを立証することが必要となる．現在はディスクバースト試験によって要求を満たすことを立証しているが，コストと時間の削減のために，構造解析による立証が望まれている．

ディスクの過回転バーストにおいて，径方向変位の増加によって慣性力が増加することで構造不安定に陥る構造不安定バーストと，材料が変形して破断ひずみに到達することで延性破壊する延性破壊バーストの二つの破壊形態が考えられる．構造解析によってこれらのバーストが発生する回転数を高精度に予測するためには，材料がネッキングするような高ひずみ領域の変形挙動や最終的な破断現象などの材料の終局挙動の考慮が重要となる．しかし，ひずみゲージなどでは試験片にネッキングが生じるような高ひずみ領域における局所的なひずみを計測することが難しく，また，単一のひずみだけでは最終破断を十分な精度で予測できない．そこで本研究では，航空エンジンディスクに多く使用されるTi-6Al-4V鍛造材製のディスクを対象に，デジタル画像相関法 ( Digital Image Correlation：DIC ) によって局所性も考慮した高ひずみ領域までの応力－ひずみ関係を取得した．またこの応力－ひずみ関係を用いた構造解析を行い，応力状態に依存する破断ひずみに基づく延性破壊クライテリアを用いて，過回転バーストに至る終局限界評価を実施した．

2.　応力ひずみ関係

2.1　引張試験のDIC計測

Ti-6Al-4V鍛造材の高ひずみ領域における応力ひずみ関係を取得するためには，試験片がネッキングしてから破断するまでの高ひずみ領域におけるひずみ計測が必要となる．ひずみゲージや伸び計では，取り付け位置や計測領域の大きさ，計測可能なひずみの上限が問題となり，破断までの局所的なひずみを取得することが困難であった．そこで，本研究ではDICを用いて引張試験における破断までのひずみ計測を実施した．DICはグレースケールデジタル画像分析によって画像上で変位量を計測し，非接触でひずみ分布を得る手法である．

本研究の引張試験のDIC計測で使用した板厚2 mm，平行部幅12.5 mmの平滑平板試験片の形状を第1図に示す．事前にディスクの予備解析を行いバースト時に重要となるひずみ速度を確認し，ひずみ速度を0.000 1 s⁻¹から1 s⁻¹まで変更して，引張試験を実施した．代表的なDIC計測結果を第2図に示す．試験片ネッキング部で局所的に集中したひずみを計測できていることが確認できた．ひずみ速度0.01 s⁻¹以上では，十分なフレームレートを確保するために高速度カメラを用いて画像を撮影した．

2.2　真応力－真ひずみ関係の作成

DICで得たひずみ分布を用いて真応力と真ひずみを取得した．第2図に示したようにひずみに局所性があるため，本研究ではネッキング部の断面における平均ひずみと平均応力を求めることで真応力－真ひずみ関係を決定した ^{( 2 )}．まず，DICによって得られた最終破断位置における軸方向ひずみε_yを幅方向に平均化したひずみ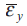 を求め，これを真ひずみε_Tとした．

ここで，Wは平行部の幅であり，xはその方向である．

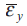
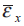
一方，真応力を取得するにはネッキング時の断面積の変化を考慮する必要がある．断面積の計算には板厚の情報が必要であるが，板厚方向の変形量はDIC計測では取得できない．そこで，軸方向と幅方向の変形量と体積一定の仮定を用いて断面積を取得した．まず，( 1 ) 式の平均化した軸方向ひずみに加えて，最終破断位置における幅方向ひずみε_xを幅方向に平均化したひずみを取得する．

ここで，塑性変形中の体積は一定と考えることで，板厚方向の平均的なひずみ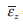は以下のように求めることができる．

よって，ネッキング部の断面積Aは，初期断面積A₀ を用いて，( 4 ) 式のように求めることができる．

本研究では，DIC計測結果を用いて ( 4 ) 式から計算された断面積Aによって試験機荷重Fを除することで，真応力σ_T を取得した．

引張試験によって得られた真ひずみ（塑性ひずみε_p ）と真応力の関係を第3図に示す．

3.　延性破壊クライテリア

3.1　応力三軸度とLode角パラメータ

金属の延性破壊は，金属材料中の介在物やミクロなボイドを起点として，応力が加わることによってボイドが成長，連結し，延性亀裂を形成することで引き起こされる ^{( 3 )，( 4 )}．このボイドの成長や連結には応力三軸度が深くかかわっており，破断ひずみに大きな影響を与える．ここで，応力三軸度ηは，静水圧応力σ_mとMisesの相当応力σ_eqの比で表され，応力の三軸性を示す．主応力3 成分σ₁，σ₂，σ₃を用いることで，応力三軸度ηは ( 6 ) 式で表される．

また，Lode角パラメータ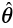は主応力空間内における応力の方位として定義されるLode角θ_Lを正規化した値であり，純せん断状態への近さを表す指標である．Lode角パラメータ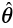は，偏差応力の第2不変量J₂と第3不変量J₃を用いて ( 7 ) 式で定義され，純せん断のときに0，一軸引張もしくは等二軸圧縮のときに1，一軸圧縮もしくは等二軸引張のときに−1となる ^{( 5 )}．

このLode角パラメータと応力三軸度によって応力状態を一意に表せる．Baiらは ( 8 ) 式で記述されるNew Fracture Locus Function ( NFLF ) によって，破断ひずみを応力三軸度ηとLode角パラメータ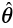の関数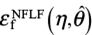として表すことができるとしている ^{( 6 )}．

ここで，D₁からD₆はNFLFの六つの未定材料定数である．NFLFは破断ひずみの応力三軸度およびLode角パラメータ依存性を高い自由度で表現できるため，本研究ではこれを用いることにした．

負荷中に生じる相当塑性ひずみ増分dε_pとNFLFで得られる破断ひずみ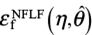 の比率を損傷度増分dDと定義する．ところで，前述のとおり金属の延性破壊では負荷中の材料内で生じたミクロなボイドが成長し，連結することで延性亀裂となる．ボイドの成長は，負荷過程で塑性ひずみεpが増加する各時刻における応力三軸度ηとLode角パラメータ 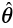の影響を受ける．そこで本研究では，負荷過程の応力三軸度およびLode角パラメータの変化履歴を考慮するために，( 9 ) 式のように負荷中のdDを積分して表される損傷度Dを用いて，D= 1.0で延性破壊が発生するとして，これをクライテリアに用いることにした ^{( 7 )}．

以降では，本クライテリアをNFLF破壊クライテリアと記述する．

3.2　クーポン試験の実施

バースト挙動の予測のためには，ディスクで生じる範囲の応力三軸度とLode角パラメータにおける破断ひずみの取得が必要となる．そこで，Ti-6Al-4V鍛造材を用いてさまざまな負荷形態，試験片形状におけるクーポン試験を実施した．本研究で実施した22 種類のクーポン試験を第1表に示す．第1表には3. 3 節で後述する解析で得られた各試験片の応力三軸度とLode角パラメータも記載している．また，各試験片の形状を第4図に示す．クーポン試験の事前の予備解析を行い，NFLFの六つの未定材料定数を決定でき，かつ広範囲の応力三軸度とLode角パラメータにおける破断ひずみを取得できるように，試験条件を決定した．

丸棒試験片や平板試験片では，試験片の破断まで一定の速度で引張変位を負荷した．切欠きの形状を丸棒試験片では5 種類，厚板平板試験片では2 種類，薄板平板試験片では4 種類用いることで，応力状態を制御した．中空切欠き丸棒試験片では，引張とねじりの2 種類の変位を同時に負荷し，その比率を変更することで応力三軸度とLode角パラメータを制御しながら負荷した．シャルピー型試験片では先行研究 ^{( 8 )} を参考に，スパン40 mmの3 点曲げ試験の途中止めと断面組織観察から，延性亀裂発生時の変形量を取得した．スモールパンチ試験片では，φ 50 mmの鋼球を試験片に押し込むことで，等二軸引張応力の状態で負荷した．

3.3　クーポン試験の解析

クーポン試験の有限要素解析を実施した．ここで，Ti-6Al-4V鍛造材の材料構成則として，2 章で構築した真応力－真ひずみ関係を用いた．

解析に用いた代表的な有限要素モデルを第5図に示す．丸棒試験片と中空切欠き丸棒試験片，スモールパンチ試験片は，軸対称ソリッド要素を用いてモデル化した．切欠き厚板や切欠き薄板などの平板試験片やシャルピー型試験片は，三次元ソリッド要素によってモデル化した．いずれの有限要素モデルにおいても，評価部近傍のメッシュサイズは0.1 mmに統一した．代表的なクーポン試験の解析で得られた荷重と変形量の関係も第5図に示す．解析は試験結果を精度良く再現しており，解析の妥当性が確認された．

解析によって，各クーポン試験の破断までの応力三軸度およびLode角パラメータを取得した．ここで，負荷過程における応力三軸度ηとLode角パラメータ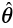の変化履歴を考慮するために，次式で表されるように塑性ひずみε_pによって破断ひずみε_f までの積分処理を行った後に平均化を施した ^{( 7 )}．

( 10 ) 式と ( 11 ) 式によって試験片の破断まで平均化した応力三軸度ηとLode角パラメータ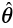を前述の第1表にまとめる．

3.4　NFLFで表す破断ひずみの作成

クーポン試験で得られた応力三軸度，Lode角パラメータと破断ひずみを用いて，NFLFを作成した．( 8 ) 式で表されるNFLFの六つの材料定数を決定するために，( 12 ) 式で定義した誤差関数Eを用いた．

ここで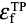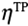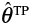，，，はクーポン試験の破断ひずみ，応力三軸度，Lode角パラメータである．( 12 ) 式の誤差関数を最小化するようにNFLFの材料定数を求めた．

NFLFを用いて作成した破断ひずみを第6図に示す．応力三軸度が低くなると破断ひずみが増加し，特にLode角パラメータの絶対値が高いほど，その傾向が強くなることが確認された．また，図中にはクーポン試験の結果を黒丸で表示しており，NFLFによる破断ひずみは，クーポン試験の結果と精度良く一致していることが確認できる．

4.　ディスクバースト評価

4.1　ディスクバースト試験

試験用の小径ディスクを対象に，バースト試験を実施した．小径ディスクの形状を第7図に示す．外径は約150 mmである．バースト試験では一定の加速度でディスクの回転数を増加させ，ディスクを過回転バーストさせた．試験中は，バースト時刻までのディスク外周部の径方向変位を計測した．高速度カメラによって撮影したバースト試験の写真を第8図に示す．第8図 - ( c ) 中のウェブ内径側の点線で囲った領域にて，ディスク表面に周方向に開口した径方向亀裂の存在を確認できた．その後，第8図 - ( d ) において亀裂が外径側に進展し，最終的に- ( e ) に示すバーストに至った．

4.2　ディスクバースト解析

小径ディスクを対象にバースト解析を実施した．軸対称ソリッド要素を用いてモデル化した．Ti-6Al-4V鍛造材の材料構成則として，2 章で構築した真応力－真ひずみ関係を用いた．

4.3　考察

ディスクバースト試験およびディスクバースト解析で得られた回転数とディスク外周部の径方向変位の関係を第9図に示す．バースト試験では，径方向変位の急激な増加に伴う慣性モーメントの急増加に起因して，回転加速度が緩やかに減少して最大回転数に到達し，その後は回転数の低下が生じることが分かった．バースト解析では，回転数の低下までは再現していないものの，最大回転数到達までの変形量を極めて高い精度で予測できることが分かった．

続いて，本ディスクのバースト形態について検討した．バースト解析より，本ディスクにおいて慣性力の増加によってディスク内部で力の釣り合いを満たせなくなり，構造体として成立せずに加速度的な変形増大が生じる構造不安定点が存在することが判明した．この構造不安定点におけるディスク内での破断の有無を検証するために，構造不安定点でのディスクの損傷度分布を確認した結果を第10図に示す．損傷度Dが最大となる位置はハブの内部であり，試験で亀裂が観測されたウェブ内径側に近い位置であった．このときの損傷度の最大値はD = 0.76であり，1.0を下回っていることから構造不安定点で延性破壊が発生していないことが分かった．このことから，本ディスクのバースト形態は構造不安定バーストであることが明らかとなった．

バースト試験で得られた破壊起点を予測できるかを検証する目的で，構造不安定が発生した後に生じる材料の延性破壊について検討した．材料の損傷度Dが1.0を超えたときの損傷度分布を第11図に示す．損傷度の最大位置は構造不安定発生時点の第10図よりも外径側に移動し，ウェブ内径側の表面で最大となった．これは，ディスクバースト試験における亀裂観察部と極めて近い位置であった．ここで，同時刻における相当塑性ひずみの分布を第12図に示す．損傷度と異なり，塑性ひずみはボアで最大となっていた．本ディスクにおいて，応力三軸度とLode角パラメータの状態がボアとウェブ内径側で異なっており，ウェブ内径側において破断ひずみ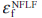が小さくなることで，損傷度Dが最大になることが判明した．

以上より，本研究にて構築した手法を用いることで，ディスクの過回転バーストを対象とした構造解析によって，精度良く終局限界挙動を評価できることが示された．

5.　結言

Ti-6Al-4V製のディスクを対象に，過回転バーストに至る終局限界評価手法を構築した．以下に内容をまとめる．

1. ネッキングが生じるような高ひずみ領域での真応力－真ひずみ関係を取得するために，DICによるTi-6Al-4V鍛造材の引張試験中のひずみ計測を行った．DIC計測で得られたひずみ分布から，ネッキング部の真応力－真ひずみ関係を取得した．
2. Ti-6Al-4V鍛造材の延性破壊クライテリアを取得するために，応力三軸度とLode角パラメータを制御した22 種類のクーポン試験を実施した．各クーポン試験結果と有限要素法による解析結果から，応力三軸度とLode角パラメータに対応した破断ひずみを同定した．また，これらの結果を用いて，Ti-6Al-4V鍛造材におけるNFLFに基づく破壊クライテリアを作成した．
3. 小径ディスクの過回転バーストを対象に，終局限界評価を行った．DICを用いて作成した真応力－真ひずみ関係を用いることで，バースト試験で生じる変形量を解析によって極めて高い精度で予測できた．また，NFLFに基づく破壊クライテリアを用いることで，ディスクの破壊起点を精度良く予測できることを示した．

昨今，開発期間の短縮や試験費用の削減のため，Certification by Analysisの議論が活発になっている．航空エンジンの競争力強化のために解析によるディスクの認証取得が望まれており，これを実現するためには本技術を用いた設計手法の確立が必須となる．

　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　　　 　　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　

第63巻 第2号 特集 社会課題の解決を支える基盤技術の進化